Object Oriented Programming (OOP) in Python

Author: Spencer Lyon

So far in your python training you have been introduced to many different ideas and concepts. You have probably heard the term “object” a few times, without really understanding what it means. This being true, the code you have written up to this point has been object based – you have passed around objects in your scripts, used them in expressions, called their methods, ect. In order for your code to be truly object-oriented you need to start to defining your own classes.

This lab will teach you the basics of OOP and get you some hands-on experience using them in your code.

Introduction

The term object oriented programming encapsulates a new way of thinking about your code. Instead of having your programs simply being a list of instructions to be executed in sequential order when your script is run, OOP takes a more abstract approach that focuses more on the relationship between the different parts of your code and which tasks should be performed by each part.

Why use OOP?

At this point, you might be wondering why you need to learn a whole new way to think about programming. Hasn’t what you have been doing all along good enough? The answer is ... kind of. What you have been doing up to this point, writing out a list of instructions for the interpreter to execute, is known as procedural programming. It is the foundation of modern computer science. For this reason old, powerful languages like C and Fortran, which do not support OOP by themselves, are classified as procedural programming languages. However, there has been a clear shift in mainstream programming toward newer languages that do support OOP. Some examples are Java, C++, Python (surprise!), Ruby, C#, Objective-C, and many more. So why are more and more programmers using OOP in their code? I can think of 2 (there are definitely more) distinct advantages an OOP approach has over a standard procedural approach.

1. Code re-usability: This is probably the biggest plus for OOP. With OOP you define objects that have certain properties. If you then realize that you need an object with very similar features, you can simply subclass the original object and save your self from writing all that code over again. Although copy/paste is a plausible form of code reuse, it quickly becomes difficult to manage with larger, more complicated projects. As an example, say you wanted to code an OLG model. One way to do this from and OOP persepective might be to define the following classes with respective properties:

   • Agent:

     • age property that specifies the agent’s age.
     • utility method (function) that returns the utility for a given state of the economy and a given choice of consumption and labor supply.
     • consume method that evaluates the optimal amount of food to consume given a current state of the economy – uses the utility method.
     • work method that returns the optimal amount of labor to supply given the current state of the economy – uses the utility method.

   • Firm:

     • produce method that returns how much of a good is produced given the state of the economy
     • captial property that specifies the aggregate capital stock in the current period
     • labor property that specifies the total supply of labor in the current period

   • Economy:

     • period property that keeps track of the time period
     • agents list that contains a list of all current agents
     • firms list that contains a list of all current firms
     • shocks dictionary of pandas.Series objects that specify the exogenous shocks over time
     • endog_state property of a pandas.DataFrame containing the endogenous state data over time.
     • gather_choices method that sends each object in the the agents and firms lists the current data and receives the choice variables.

   You could then create multiple instances of the Agent class to represent agents of different ages in your economy. You would also need at least one Firm instance to represent the other half of the market and a single Economy instance to keep everything organized (you could also have methods in the Economy class that would gather consumption, labor supply and production results from each of the other instances in the economy).

2. Unite data and functionality: An object is really just a generic container in which you can place data and different methods that act on that data. You have already seen this benefit in the BSplineBasis class you wrote earlier. Had you tried to do this without object oriented programming, every function that makes up the spline (generating knots, defining basis functions, evaluating or plotting the basis functions, ect.) would have had to have additional arguments that specify the details of the spline (things like degree, number of knots, the knot vector or list of basis functions, ect.). Even in this small example you can see how this could get out of hand with a bigger problem.

An Outline - OOP in Python

Python is, at its core, an object oriented programming language. Everything you use or variable you define in python is an object. You can verify this using the type function. I will demonstrate below.

In [11]: type(42)
Out[11]: int

In [12]: type(1.2)
Out[12]: float

In [13]: type('foo')
Out[13]: str

In [14]: type([1, 3, 4])
Out[14]: list

In [15]: type({1:3, 2:4})
Out[15]: dict

In [16]: type(('b', [3], 4))
Out[16]: tuple

In [17]: type(np.array([1, 3, 4]))
Out[17]: numpy.ndarray

In [18]: type(pd.Series([1, 2]))
Out[18]: pandas.core.series.Series

Every object in python has characteristics that are broken into two main categories: 1. [data] attributes, and 2. methods. Attributes are the specific pieces of data that make one object unique from another. Methods are python functions that act on that data. As an example consider a python list:

In [19]: a = [1, 2, 'string', 2.3]

The data for this list are the items in the list. In this example they are the int 1, the int 2, the str ‘string’, and the float 2.3. Lets take a look at what methods are available to a list:

In [20]: not_special = lambda x: not x.startswith('__')

In [21]: filter(not_special, dir(a))
Out[21]: 
['append',
 'count',
 'extend',
 'index',
 'insert',
 'pop',
 'remove',
 'reverse',
 'sort']

Calling any of these methods will apply that python function to the list and alter it somehow:

In [22]: a
Out[22]: [1, 2, 'string', 2.3]

# reverse order of data
In [23]: a.reverse()

In [24]: a
Out[24]: [2.3, 'string', 2, 1]

# return the last item in the list and remove it from the list
In [25]: a.pop()
Out[25]: 1

# see, it's gone!
In [26]: a
Out[26]: [2.3, 'string', 2]

The class keyword is used to define new types of objects in python. A class definition will describe what kind of data it stores and what functions are available for acting on this data (functions defined within classes are referred to as methods). On their own, class definitions are not useful, just like defining a function without calling it is not useful. To make use of a class, you need to create an object of that class or type. These are known as instances of the class. It is most common for each instance of a class to have its own unique data, while the methods are common across instances.

Throughout the rest of this lab we will focus on how to create and use new objects we define.

Defining Custom Classes

As noted above, new classes are defined using the class keyword. Imagine I wanted to create a class that represented a die. I would begin like this:

 class Die(object):
    pass

I will break this down one word at a time:

• class: like the keyword def for functions, this tells python I am about to define a new class
• Die: This is the name of the new class. It is common convention in python to have class names where the first letter in each word is capitalized, and there are no spaces in multi-word class names (e.g. DataFrame follows convention)
• (object): This tells us that we are going to be subclassing the built-in python class object. We will discuss sublcasses more later so don’t worry too much about this for now. If you don’t know what you want the parent class to be, it is convention to put object here. Also note the :.
• pass: A python keyword that allows us to not write anything in the body, but also not have the interpreter raise an IndentationError when the file is executed.

The __init__ method

After having told python that I will be defining a new class, I need to tell it what should happen when a new instance of this class is created. This happens in the __init__ method (the two leading and trailing underscores are important and we will talk more about them shortly). This is the function that is called when we are creating a new class. For the Die, it might looks something like this:

class Die(object):
    def __init__(self, sides=6, dots=None):
        self.nsides = sides
        self.dots = dots

Note

In all the examples in this lab I will omit docstrings and I may, at times, number lines in a non PEP8 compliant way as I have done above. I am doing this just for instructional purposes. When actually writing code that will be executed I wouldn’t do this.

I will break this down one line at a time:

• [2] Tells python that I am going to be defining the __init__ method. The first argument to ALL class methods is the keyword self. The things that follow will be unique to the particular class. In this case we can pass in the number of sides the current value of the dots.
• [3] Set the attribute nsides and have it be equal to the sides parameter to the function
• [4] Set the attribute dots and have it be equal to the dots parameter to the function

Adding methods

At this point, I could create an instance of the Die class, but it wouldn’t be able to do much. Before we do that I will add one more method: roll. As I am sure you can guess, this method will simulate the rolling of the die and update the dots parameter of the object.

from random import randint
class Die(object):

    def __init__(self, sides=6, dots=None):
        self.nsides = sides
        self.dots = dots

    def roll(self):
        self.dots = randint(1, self.nsides)

Explanation by line:

• [1] import the randint function from the python random module
• [8] Begin definition of roll method. Notice the passing of self as the only argument and the single line of spacing between class methods
• [9] Update the self.dots attribute to be a new random integer between 1 and the self.nsides attribute.

I am now going to create a new instance of my Die class and roll it a few times.

In [27]: d = Die(6)  # [1]

In [28]: d.nsides    # [2]
Out[28]: 6

In [29]: d.dots      # [3]

In [30]: d.roll()    # [4]

In [31]: d.dots      # [5]
Out[31]: 1

In [32]: d.roll()    # [6]

In [33]: d.dots      # [7]
Out[33]: 6

In [34]: d           # [8]
Out[34]: <__main__.Die at 0x111a79610>

Explanation by line:

• [1] Create a new instance of the Die class with 6 sides. Store it in a variable named d.
• [2] Check the d.nsides attribute
• [3] Access the dots attribute of the d. Notice that it is not printed because it’s current value is the default to __init__: None
• [4] Call the roll method of the Die class and update d.dots
• [5] Check the value of d.dots
• [6] Call the roll method of the Die class and update d.dots
• [7] Check the value of d.dots
• [8] A very unhelpful string representation of our object (see __repr__ and __str__ below.)

Notice that when I am defining the class or calling a method that I treat the self parameter to the methods as if is isn’t there. I tell the __init__ methods the value of its sides argument by passing it as the first argument to Die.

Other Special Methods

In a python class having a method name start and end with two underscores tells python that it is a special or magic method. These methods are usually used to allow access to object’s data or functions via python keywords or operators. This is a bit abstract and I best understood by example. Below is a table of many of the most common special methods:

Method Name	Description	Usage
__repr__	Returns the string printed to the screen when an object is not assigned a name	d
__str__	Called when str or print is called on the object	str(d) or print(d)
__sub__	Called when using -	d - d
__ge__	Called when using `` >``	d1 > d2
__getitem__	Called when trying to index object	d1[2]
__cmp__	Implements the full suite of comparison operators	d > d or d == d1, ect.
__rsub__	Called when using -=	d -= 1
__len__	Called when using len()	len(d)
__call__	Called when using d()	d()

I have barely scratched the surface of the special methods in python. For example, in addition to __sub__ there are the __mul__, __div__, __add__ methods that implement other basic mathematical operations. Another example is that in addition to __ge__, there are 5 other comparison operator methods to be used when calling <, <=, >=, ==, and !=. See the official Python docs on special methods and this great site on Operator Overloading for more in-depth examples.

Let’s add a few of these to the Die class:

class Die(object):
    def __init__(self, sides=6, dots=None):
        self.nsides = sides
        self.dots = dots
        if self.dots is None:
            self.roll()

    def __repr__(self):
        return str(self.dots)

    def __str__(self):
        return self.__repr__()

    def __unicode__(self):
        return self.__repr__()

    def __lt__(self, other):
        return self.dots < other.dots

    def __le__(self, other):
        return self.dots <= other.dots

    def __eq__(self, other):
        return self.dots == other.dots

    def __ne__(self, other):
        return self.dots != other.dots

    def __gt__(self, other):
        return self.dots > other.dots

    def __ge__(self, other):
        return self.dots >= other.dots

    def roll(self):
        # Make sure we roll between 1 and nsides
        self.dots = randint(1, self.nsides)
        return self.dots

I will now test some of these out:

In [35]: d1 = Die(6, 5)

In [36]: d2 = Die(6, 4)

In [37]: d1
Out[37]: 5

In [38]: d2
Out[38]: 4

In [39]: d1 > d2
Out[39]: True

In [40]: d2 <= d1
Out[40]: True

In [41]: d1 == d2
Out[41]: False

Subclassing

Another term in object-oriented programming is subclass. This term means that one class is a child, or inherits from another class. When this happens, all methods and data that are part of the first, super, or parent class become part of the subclass. There is the added benefit, however that you can override the default behavior of the parent class.

As an example, suppose we wanted to create a new class called StandardDie. This class would be a subclass of the Die class we wrote earlier, but we would only allow it to have 6 sides. Suppose also that we wanted to update the printing system for the class and give it some very basic ASCII art representing the face of the die. I have done this below:

class StandardDie(Die):
    def __init__(self, dots=1):
        super(StandardDie, self).__init__(sides=6, dots=dots)
        self.dots = dots
        self.roll()

    def __repr__(self):
        if self.dots == 1:
            msg = "\n x\n"
        elif self.dots == 2:
            msg = "x\n\n  x"
        elif self.dots == 3:
            msg = "x\n x\n  x"
        elif self.dots == 4:
            msg = "x  x\n\nx  x"
        elif self.dots == 5:
            msg = "x  x\n x\nx  x"
        elif self.dots == 6:
            msg = "x  x\nx  x\nx  x\n"
        else:
            msg = ""
        return msg

We will test to make sure the StandardDie class has all the comparison operators and roll function that were only implemented in the Die class, but also make sure that the new printing system took hold:

In [42]: d1 = Die(6, dots=4)

In [43]: d2 = StandardDie(4)  # remember only dots is a parameter here

In [44]: d1
Out[44]: 4

In [45]: d2
Out[45]: 
x  x
x  x

In [46]: d1 > d2
Out[46]: False

In [47]: d1 == d2
Out[47]: True

In [48]: d2.roll()
Out[48]: 4

In [49]: d2
Out[49]: 
x  x
x  x

In [50]: def check_inheritance(x):
   ....:     return isinstance(x, Die), isinstance(x, StandardDie)
   ....:

# Should be True, False
In [51]: check_inheritance(d1)
Out[51]: (True, False)

# Both True
In [52]: check_inheritance(d2)
Out[52]: (True, True)

Yhatzee Example

I have taken this dice example and extended it to create the game Yhatzee. You can download the file here, but I will include the other pieces here for completeness.

from random import choice, randint, shuffle
from string import digits
import re
import numpy as np
import pandas as pd

_parse_selection = re.compile('(\d)')

def _random_name():
    return 'Player' + ''.join(choice(digits) for i in range(2))


# Score card constants
_top_index = ['Ones', 'Twos', 'Threes', 'Fours', 'Fives', 'Sixes',
              'Bonus']

_bot_index = ['ThreeOfKind', 'FourOfKind', 'FullHouse', 'SmStraight',
              'LgStraight', 'Yhatzee', 'Chance', 'Bonus']

_arrs = [['Top'] * len(_top_index) + ['Bottom'] * len(_bot_index) + ['Total'],
         _top_index + _bot_index + ['']]

_ind = pd.MultiIndex.from_arrays(_arrs)


class Die(object):
    def __init__(self, sides=6, dots=None):
        self.nsides = sides
        self.dots = dots
        if self.dots is None:
            self.roll()

    def __repr__(self):
        return str(self.dots)

    def __str__(self):
        return self.__repr__()

    def __unicode__(self):
        return self.__repr__()

    def __lt__(self, other):
        return self.dots < other.dots

    def __le__(self, other):
        return self.dots <= other.dots

    def __eq__(self, other):
        return self.dots == other.dots

    def __ne__(self, other):
        return self.dots != other.dots

    def __gt__(self, other):
        return self.dots > other.dots

    def __ge__(self, other):
        return self.dots >= other.dots

    def roll(self):
        # Make sure we roll between 1 and nsides
        self.dots = randint(1, self.nsides)
        return self.dots


class StandardDie(Die):
    def __init__(self, dots=1):
        super(StandardDie, self).__init__(sides=6, dots=dots)
        self.dots = dots
        self.roll()

    def __repr__(self):
        if self.dots == 1:
            msg = "\n x\n"
        elif self.dots == 2:
            msg = "x\n\n  x"
        elif self.dots == 3:
            msg = "x\n x\n  x"
        elif self.dots == 4:
            msg = "x  x\n\nx  x"
        elif self.dots == 5:
            msg = "x  x\n x\nx  x"
        elif self.dots == 6:
            msg = "x  x\nx  x\nx  x\n"
        else:
            msg = ""
        return msg


class Dice(object):
    def __init__(self, numdice=5, sides=6, die_class=Die):
        self.nsides = sides
        self.ndice = numdice
        self.dice = [die_class(6) for i in xrange(numdice)]

    @property
    def dots(self):
        return [i.dots for i in self.dice]

    def __repr__(self):
        msg = 'The dice are:\n\n'
        msg += str('\n' +'-'*8 + '\n').join([repr(i) for i in self.dice])
        msg += '\n\n'
        msg += 'index: value\n'
        msg += '\n'.join(['    %i: %i' % (i, j) for i, j in enumerate(self.dots)])
        return msg

    def __str__(self):
        return self.__repr__()

    def __unicode__(self):
        return self.__repr__()

    def __len__(self):
        return len(self.mdots)

    def __getitem__(self, index):
        return self.dice[index]

    def __setitem__(self, index, value):
        self.dice[index].dots = value

    def __iter__(self):
        return iter(self.dice)

    def roll(self, index='all'):
        if index == 'all':
            for i in self.dice:
                i.roll()

        elif isinstance(index, int):
            # Just roll 1
            self.dice[index].roll()

        elif isinstance(index, list):
            # Roll all in the index list
            for i in index:
                self.dice[i].roll()


class YhatzeeScoreCard(object):
    def __init__(self, players=None):
        """
        Score card for Yhatzee.

        Parameters
        ----------
        players : iterable of strings
            A list, tuple, array, ect. containing Player Instances
        """
        if players is None:
            # Just make 2 random names
            players = [_random_name() for i in xrange(2)]

            # TODO: Should we use a DataFrame here or just roll our own class?
            self.card = pd.DataFrame(np.zeros((len(_ind), len(players))),
                                     index=_ind, columns=players)
        else:
            # Use the Players' score_card as columns
            self.card = pd.DataFrame([i.score_card for i in players]).T

    def __repr__(self):
        # Just use pandas
        return repr(self.card)

    def __str__(self):
        return self.__repr__()

    def __unicode__(self):
        return self.__repr__()

    def update(self, players):
        self.card = pd.DataFrame([i.score_card for i in players]).T


class YhatzeeScorer(object):
    def __init__(self, dice):
        # make a series out of the dice
        self.dice = dice
        self.d_Series = pd.Series(dice.dots)
        self.v_counts = pd.DataFrame(self.d_Series.value_counts(),
                                     index=range(1, 7))
        self.v_counts = self.v_counts.fillna(0)

    def score_numeric(self, num):
        """Computes numeric score for num (top of scorecard)"""
        vc = self.v_counts.copy()
        vc[0] = vc[0].values * vc.index.values
        return int(vc.ix[num])

    def _score_3_of_kind(self):
        """Tries to compute score of 3 of a kind"""
        if int(self.v_counts.max()) < 3:
            return 0
        else:
            return self.d_Series.sum()

    def _score_4_of_kind(self):
        """Tries to compute score of 4 of a kind"""
        if int(self.v_counts.max()) < 4:
            return 0
        else:
            return self.d_Series.sum()

    def _score_full_house(self):
        """Tries to compute score of full_house"""
        sort_counts = self.v_counts.sort(0, ascending=0)
        if sort_counts.iloc[0] == 3 and sort_counts.iloc[1] == 2:
            return 25
        else:
            return 0

    def _score_sm_straight(self):
        """Tries to compute score of small straight"""
        t1 = np.array([1, 2, 3, 4])
        t2 = np.array([2, 3, 4, 5])
        t3 = np.array([3, 4, 5, 6])
        n_zero = self.v_counts[0].nonzero()[0] + 1
        if n_zero.size > 3:
            c1 = np.array(n_zero == t1).all()
            c2 = np.array(n_zero == t2).all()
            c3 = np.array(n_zero == t3).all()
            if c1 or c2 or c3:
                return 30
        return 0

    def _score_lg_straight(self):
        """Tries to compute score of large straight"""
        t1 = np.array([1, 2, 3, 4, 5])
        t2 = np.array([2, 3, 4, 5, 6])
        n_zero = self.v_counts[0].nonzero()[0] + 1
        if n_zero.size == 5:
            if all(n_zero == t1) or all(n_zero == t2):
                return 40
        return 0

    def _score_yhatzee(self):
        """Tries to compute score of yhatzee"""
        if int(self.v_counts.max()) == 5:
            return 50
        else:
            return 0

    def _score_bonus(self):
        """Tries to compute score of 3 of a kind"""
        pass

    def _score_chance(self):
        return self.d_Series.sum()

    def score_special(self):
        """Uses the '_' methods to score the bottom"""
        pass

    def score_all(self, c_name=0):
        # Blank score_card to fill in
        temp_sc = pd.DataFrame([0]*16, index=_ind, columns=[c_name])
        temp_sc = temp_sc.drop(('Top', 'Bonus'))
        temp_sc = temp_sc.drop(('Total', ''))
        for i in range(6):
            temp_sc.ix['Top', _top_index[i]] = self.score_numeric(i + 1)

        temp_sc.ix['Bottom', 'ThreeOfKind'] = self._score_3_of_kind()
        temp_sc.ix['Bottom', 'FourOfKind'] = self._score_4_of_kind()
        temp_sc.ix['Bottom', 'FullHouse'] = self._score_full_house()
        temp_sc.ix['Bottom', 'SmStraight'] = self._score_sm_straight()
        temp_sc.ix['Bottom', 'LgStraight'] = self._score_lg_straight()
        temp_sc.ix['Bottom', 'Yhatzee'] = self._score_yhatzee()
        temp_sc.ix['Bottom', 'Chance'] = self._score_chance()

        return temp_sc


class Player(object):
    def __init__(self, name=None):
        if name is None:
            name = _random_name()

        self.name = name
        self.score_card = pd.Series(np.zeros(len(_ind)), index=_ind, name=name)
        self.have_chosen = set()

    #### Operators to see how this Player's score compares to others
    def __lt__(self, other):
        return self.score < other.score

    def __le__(self, other):
        return self.score <= other.score

    def __eq__(self, other):
        return self.score == other.score

    def __ne__(self, other):
        return self.score != other.score

    def __gt__(self, other):
        return self.score > other.score

    def __ge__(self, other):
        return self.score >= other.score

    ### Let's print it real good!
    def __repr__(self):
        # Just use pandas, they print pretty good
        return repr(self.score_card)

    def __str__(self):
        return self.__repr__()

    def __unicode__(self):
        return unicode(self.__repr__())

    def _prep_score_chooser(self, dice):
        # Get the scorer
        scorer = YhatzeeScorer(dice)

        # Have him score everything
        df = scorer.score_all()
        df = df.rename_axis({0:'new'})
        df['existing'] = self.score_card
        df['index'] = range(df.shape[0])
        df = df.reindex(columns=['existing', 'new', 'index'])
        return df

    def _get_ind_choice(self, df):
        print(df)
        # Let user choose which score to keep
        ind = raw_input('Choose index of score you want to keep: ')

        ind = self._verify_ind_choice(ind)
        if ind is None:
            ind = self._get_ind_choice(df)

        return ind

    def _verify_ind_choice(self, ind):
        try:
            ind = int(ind)
            return ind
        except:
            print("Couldn't convert your choice to an integer, try again")
            return None

    def choose_score(self, dice):
        df = self._prep_score_chooser(dice)

        success = False
        while not success:
            ind = self._get_ind_choice(df)
            i_ind = df[df['index'] == ind].index

            if self.score_card.ix[i_ind] == 0 and not ind in self.have_chosen:
                # good to go
                try:
                    self.score_card.ix[i_ind] = df[df['index'] == ind]['new']
                    success = True
                    self.have_chosen.add(ind)
                except IndexError:
                    print("Invalid selection. Must be in [0, 13]")
            else:
                print("Can't replace previous score (even if it was 0), "
                      + "make selection again")
                success = False


class YhatzeeManager(object):
    def __init__(self, players, score_card, scorer):
        self.players = players
        self.score_card = score_card
        self.scorer = scorer

        # Keep track of what round we are on (only 13 number in yhatzee)
        self.round = 0

        # Get some dice for the game
        self.dice = Dice(5, 6, StandardDie)

        # Randomize turn order
        shuffle(self.players)

    def _get_die_selection(self):
        try:
            play_str = raw_input('Give index of which dice to re-roll '+
                             '(numbers separated by commas or spaces or ' +
                               'type (c) to check score_card): ')

            to_roll = [int(i) for i in _parse_selection.findall(play_str)]

            if play_str == 'c':
                print(self.score_card)
                self._get_die_selection()

        except SyntaxError:
            # Player doesn't want to
            to_roll = None

        return to_roll

    def _do_roll(self, n_roll, index='all'):
        dice = self.dice
        # Roll the dice
        dice.roll(index)

        # Show them and get selection
        print(dice)

        if n_roll < 3:
            # only on first or second roll
            rollers = self._get_die_selection()

        else:
            rollers = None

        return rollers

    def _do_turn(self, player):
        dice = self.dice
        print('\n\n%s it is your turn' % player.name)

        n_rolls = 1
        rollers = self._do_roll(n_rolls)

        if rollers is None:
            player.choose_score(dice)
        else:
            n_rolls = 2
            rollers = self._do_roll(n_rolls, rollers)

        if rollers is None:
            player.choose_score(dice)
        else:
            n_rolls = 3
            self._do_roll(n_rolls, rollers)

        player.choose_score(dice)
        self.score_card.update(self.players)

    def _check_bonuses(self):
        bonuses = (self.score_card.card.xs('Top').drop('Bonus').sum() >= 63)
        self.score_card.card.ix['Top', 'Bonus'] = bonuses * 35

    def play_game(self):
        while self.round < 13:
            for p in self.players:
                self._do_turn(p)

            self._check_bonuses()
            self.round += 1
            print('\n\n\n')
            print('=' * 78)
            print('=' * 78)
            print('After round %i the score is: ' % (self.round))
            self.score_card.card.iloc[-1] = self.score_card.card.sum()
            print(self.score_card)

        winner = self.score_card.card.sum().idxmax()

        print('\n\n')
        print('!' * 78)
        print('!' * 78)
        print('And the winner is...' + '\n'*5)
        print(winner)


def run_test_game():
    the_dice = Dice(5, 6, StandardDie)
    p1 = Player('Spencer')
    p2 = Player('Chase')
    score_card = YhatzeeScoreCard([p1, p2])
    scorer = YhatzeeScorer(the_dice)
    manager = YhatzeeManager([p1, p2], score_card, scorer)
    manager.play_game()

Todo

Using the provided yhatzee game as an example, create the dice game farkle. You can find the Farkle rules at the linked website. A lot of the logic for prompting players and controlling the game is shown in the yhatzee example.

Note

For this problem and the ones to follow you may need to search the web for more guidance and examples of OOP in practice. I have only included this one example by design, as I feel that at this point in your programming careers you should learn to be comfortable searching for answers on your own. We are, of course, willing to help, but we encourage you to do as much as you can with your fellow boot-campers and the internet.

Distribution Families

As you learned during an economics lecture earlier in bootcamp, there are many different distributions. Many of these distributions are related in a tree-like manner. Below is an image of a distribution tree for the skewed generalized T distribution family:

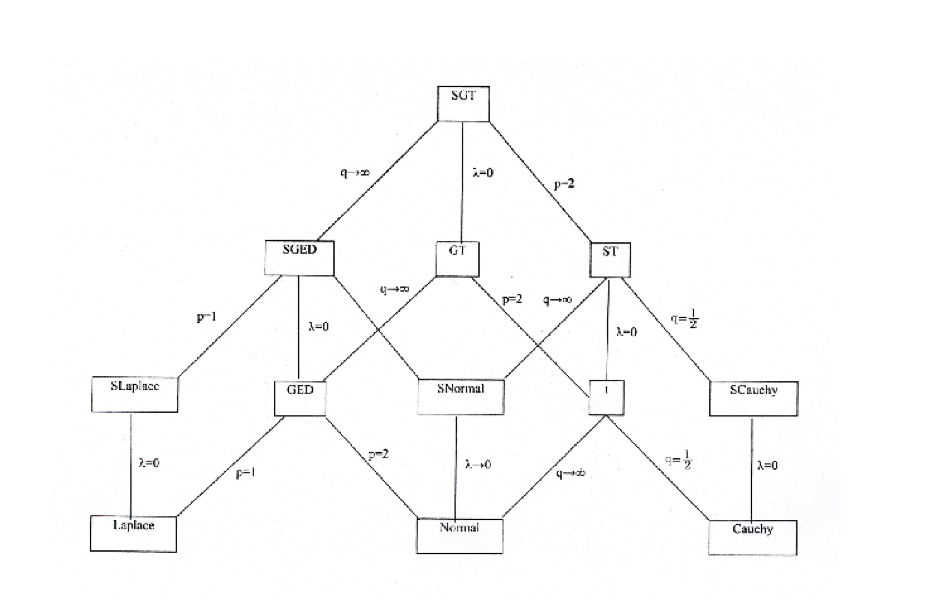
The pdf for the SGT (top of the tree) is given below:

\[SGT(\epsilon; \lambda, s, p, q) = \frac{p}{2 s q^{1/p} \beta \left(\frac{1}{p}, q \right) \left(1 + \frac{|\epsilon|^p}{q s^p (1 + \lambda \text{sign}(\epsilon))^p} \right)^{q + 1 / p}}\]

where \(\beta(a, b)\) is the beta function of \(a\) and \(b\).

Todo

Implement the entire SGT from the diagram. For each distribution you need to have attributes representing the support and, when possible, first two moments (mean and standard deviation) of the distribution. You must also have methods for the pdf of the distribution and for the cdf. Note that often the cdf has no closed-form representation. In cases such as these, approximate the cdf numerically using an integration routine like that found in scipy.integrate.quad. Get the limits of integration using the information on the support you included as an attribute for the class.

Hint: By far the easiest way to do this problem is to come up with a good implementation for the distribution at the top of the tree, in this case the SGT. You can then work your way down the tree by subclassing the more general distributions and pinning parameters down, similar to how I subclassed Die when I created StandardDie.

Hint2: You will find the function scipy.special.beta useful.

Economic Application

Disclaimer: This problem comes from a working paper by Christian Baker, Jeremy Bejarano, Rick Evans, Ken Judd, and Kerk Phillips (they might be good people to ask for help with understanding the problem).

In the working paper, they develop a sales tax model that features households and the government (partial equilibrium because they don’t compute the production side of the market). In this section of the lab, we will ask you to implement the household’s problem using the object oriented concepts you have learned in the lab.

The Model

Let the economy be characterized by \(I\) different consumption goods \(c_i\), where \(i=1, 2,...I\). Define aggregate consumption \(C\) by the constant elasticity of substitution (CES) aggregator:

\[C \equiv \left(\sum_{i=1}^I \alpha_i(c_i - \bar{c}_i)^{\frac{\eta - 1}{\eta}} \right) ^{\frac{\eta}{\eta - 1}}\]

where \(\eta \ge 1\) is the elasticity of substitution among all of the consumption goods, \(\alpha_i \in [0, 1]\) is the weight on the consumption of each type of good with \(\sum_i \alpha_i = 1\), and \(\bar{c}_i \ge 0\) is a minimum level of consumption for each type of good. The constant relative risk aversion (CRRA) utility function for the individual with CES preferences over consumption is the following:

\[u(C) = \frac{C^{1 - \gamma} - 1}{1 - \gamma}\]

where the aggregate consumption of an individual \(C\) is defined above and \(\gamma\) is the coefficient of relative risk aversion.

Let the price of consumption good \(i\) be determined by the competitive equilibrium assumption of marginal cost pricing with the additional sales tax levied on good \(i\). If \(mc_i\) is the marginal cost of producing good \(i\) and \(\tau_i\) is the sales tax rate on good \(i\), then competitive equilibrium implies that he price of each consumptino good \(p_i\) is given by

\[p_i = (1 + \tau_i) mc_i\]

We can normalize the marginal cost of each good to unity \(mc_i = 1\) for all \(i\) by simply changing the units of each good. So the price of each good can be simplified to its normalized version.

\[p_i = 1 + \tau_i\]

Given a nominal wage of \(w\), the household budget constraint is:

\[\sum_{i=1}^I (1 + \tau_i) c_i \le w\]

The household’s problem is to choose a consumption basket \(\{c_i\}_{i=1}^I\) to maximize utility subject to this budget constraing. In this example, we will allow consumers to be heterogeneous in terms of their elasticity of substitution \(\eta\) among different consumption goods and in terms of income \(w\). So \(\theta = (\eta, w) \in \Theta = [1, \infty) \times (0, \infty)\). Let the joint distribution over consumer types in the economy be \(\Gamma(\eta, w) = \Gamma(\eta) \Gamma(w)\), where \(\eta \sim ([\eta_{min}, \eta_{max}])\) and \(w \sim GB2(a, b, p, q)\).

now we can write the consumers optimization problem in terms of vectors of variables,

\[\max_c u(\boldsymbol{c}; \eta, w, \tau) \text{ s.t. } w \ge \sum_{i=1}^I (1 + \tau_i) c_i \text{ and } c_i \ge \bar{c}_i \forall i\]

where \(\boldsymbol{c} = \{c_i\}_{i=1}^I\) and \(\tau = \{\tau_i\}_{i=1}^I\). If the budget constraint binds and \(c_i \ge \bar{c}_i\) for all \(i\), the solution to the objective function can be summarized by \(I - 1\) Euler equations:

\[\alpha_i(c_i - \bar{c}_i)^{\frac{-1}{\eta}} = \alpha_I \frac{1 + \tau_i}{1 + \tau_I}(c_I - \bar{c}_I)^{\frac{-1}{\eta}} \text{ for } i = \{1, 2, \dots, I - 1\}\]

where \(w\) and all the \(tau_i\) are introduced into this equation because good \(c_I\) is substituted out of the utility function using the budget constraint. The solution to this problem is individual consumption functions \(c_i(\eta, w, \tau)\) that are functions of consumer types (\((\eta, w)\)) and tax rates \(\tau\). This household has equilibrium utility \(u\left(\boldsymbol{c}(\eta, w, \tau) \right)\) and total taxes paid of \(r(\eta, w, \tau) = \sum_{i=1}^I \tau_i c_i(\eta, w, \tau)\).

However, it is also the case that both the budget constraing and \(c_i \ge \bar{c}_i\) are not satisfied for some sales tax schedules \(\tau\).

Todo

In order to simplify this problem, we will permit you to assume that \(I=3\). Now write a python class for the agents in this model where there are subclasses for each agent (i.e. there should be a subclass for each individual). The inputs should be a wage, elasticity of substitution (\(\eta\)), and a tax schedule. Each of these subclasses should be able to return the following: the values for consumption, capital, amount payed in taxes, and utility. The class should also be able to return the both the steady state and current values of government revenue and overall welfare (utility).

Todo

Given a discrete support for \(w\) and \(\eta\), a tax schedule \(\tau\) do some really cool stuff. Your wage and elasticty values will respectively be \((.15, .85, 1.5)\) and \((2, 2, 3)\) where each value corresponds with one of the agents. Impose two different tax regimes: first is a constant tax rate of .35 and the other is a tax bracket where \(\tau = .5\) if \(w>1\) and \(\tau = .2\) if \(w \leq 1\). For each of these cases create a table comparing each agents’ utility, overall welfare, and government revenue (you can sum their utility and tax revenue to get overall welfare and government revenue). Which tax regime do you think is better and why.